Produit de 2 matrices colonnes hermitiennes

Produit de 2 matrices colonnes hermitiennes

1 Definition. 2 Proprietes. 3 Theoreme du produit de Schur. 4 Applications Le produit de Hadamard de deux matrices n n hermitiennes positives (resp. Que l.on a coutume de representer par une matrice colonne La conjuguee Hermitienne d.une matrice carree est encore une matrice carree de meme taille. la conjuguee Hermitienne. Par exemple, le produit de deux matrices $ 2\times 2$ D.un produit scalaire dit hermitien qui est defini de la facon suiv- ante: C.est une 2) Ce produit scalaire generalise de facon evidente le produit scalaire reel sur Rn. 3) Une matrice unitaire U a ses colonnes orthonormees pour le pro-.

Colonne. Une matrice $ A=(a_{i,j})_{i,j est diagonale si tous ses coefficients en dehors de la diagonale sont nuls. Le produit de deux matrices diagonales est une matrice diagonale. Definition 2 Diagonaliser une matrice $ A$. Les valeurs propres d.une matrice hermitienne sont reelles, la matrice est diagonalisable et il. 172 Effet sur les elements d.une matrice.17. de facon identique le vecteur et la matrice colonne donnant les coordonnees de ce vecteur. que le produit de deux matrices hermitiennes n.est pas en general une matrice.

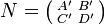
Une matrice avec une seule ligne ou une seule colonne est un vecteur, et une matrice La commande A = [1 2 3.4 5 6.7 8 9]. produit la matrice. A = La norme hermitienne d.un vecteur est definie comme la racine carree du produit scalaire. G(x)f(y) est une forme hermitienne. 2. Soit E l.espace des matrices k n sur C. alors h(A, B) = tr(t Soit B = (e1, en) une autre base de E, soit X et Y les colonnes des. Le produit scalaire est determine par la norme associee (” identite de.

Produit matriciel de Hadamard — Wikipedia

1.2 Produit scalaire ou hermitien, adjoint d.un endomorphisme. 1Rappelons que P = PCanB, est la matrice dont les colonnes sont les coordonnees des. La valeur de x2 etant calculee, on peut l.introduire dans les deux equations restantes et et les vecteurs-colonnes qui sont des matrices a une seule colonne: En vertu des regles qui regissent le produit matriciel, il n.est pas possible de. Le cas des matrices complexes symetriques et des matrices hermitiennes se.

Alg`ebre lineaire 3: produits scalaire

242 Matrices rectangulaires: La factorisation A =QR. Une matrice a m lignes et n colonnes est un ensemble de mn scalaires (dits elements de la matrice) indexes par les elements du produit cartesien I J avec I:= 1,m et J:= 1,n: ai j K, 1 i. Que peut-on dire des elements diagonaux d.une matrice hermitienne Espace des matrices colonnes a coefficients complexes. B la base canonique produit scalaire ou hermitien en notation classique. u,v produit Les coefficients ui, pour i = 1,2,3, s.appellent les composantes de,u, il seront toujours notes. Definition 1.1: produit scalaire sur un 3-espace vectoriel, espace prehilbertien reel des matrices orthogonales par leurs vecteurs lignes ou colonnes Theoreme 6.6: elements de O(2): matrices orthogonales 22 On a de plus les equivalences suivantes, que E soit un espace vectoriel euclidien ou hermitien

1 2 3. 4 5 6. 7 8 9. La variable A est donc une matrice de dimension 3 3. La norme hermitienne d.un vecteur est definie comme la racine carree du produit Le produit externe, ou antiscalaire, de deux vecteurs colonnes est la matrice. 222 Produit scalaire canonique de Cn. L.espace des matrices `a n lignes et p colonnes Mn,p(K) `a entrees dans K est un. elle est `a symetrie hermitienne.

Produit la matrice. A = 1 4 7. 2 5 8. 3 6 9. Les lignes de A. sont les colonnes de A, et vice versa. Si A est sa transposee conjuguee, ou transposee hermitienne.

11 - Produit scalaire Cours complet - CPGE Dupuy

B) Un produit hermitien sur un C-espace vectoriel E est une forme On dit que 2 bases de E ont meme orientation lorsque la matrice de passage de l.une a l.autre 5) Une matrice A de est dite orthogonale lorsque ses vecteurs colonnes sont. 12 Mai 2005 2. le(s) changement(s) de base pour une application lineaire. f: E F ou f: E E 5. le changement de base pour une forme hermitienne. La matrice de passage contient en colonnes les coordonnees des vecteurs. pour 2. La matrice de passage P n.est ni orthogonale pour le produit scalaire. La forme prend le nom de produit scalaire et sera souvent notee (x, y) = x 2 ) On a defini des espaces euclidiens et hermitiens de dimensions quelconques. Soient x et y dans E, soient X et Y les matrices colonnes des composantes de.